
16 dicembre 2019 h 20.00
Cinema Spazio Uno Firenze – via del Sole, 10
Artisti
// Tenet (nel commento: Tomás Saraceno) // Volevo nascondermi (Antonio Ligabue) // Escher Viaggio nell’infinito // Il mio capolavoro (nel commento: “Modigliani e l’avventura di Montparnasse 1920 – 2020” Livorno Museo della Città) // Lucky (nel commento: Marina Abramović) // Ella & John (nel commento: Urs Fischer) // Alla ricerca di Van Gogh //
Chi ha detto che le cose debbano per forza avere un dentro e un fuori, un sopra e un sotto?
Una striscia di carta ha due superfici; se l’appoggio sulla scrivania, le due superfici si trovano una sopra e una sotto.
Se sulla superficie superiore è rimasto attaccato un po’ di zucchero, caduto dal cucchiaino mentre lo mettevo nel caffè, e sulla superficie inferiore si trova una formica, la formica, per raggiungere lo zucchero, deve scavalcare il bordo.
Sollevo le due estremità della striscia e le incollo. La striscia è diventata un cilindro; ha due superfici, una interna e una esterna, separate da due bordi.
Ora lo zucchero si trova dentro (sulla superficie interna del cilindro); la formica si trova fuori (sulla superficie esterna).
Anche questa volta, per raggiungere lo zucchero, la formica deve necessariamente scavalcare il bordo.
Non c’è altra possibilità; se si limita ad andare avanti, non uscirà mai dalla superficie esterna del cilindro, non raggiungerà mai lo zucchero sulla superficie interna.
Se, però, prima di incollare tra loro le estremità della striscia di carta, ruoto una di esse di 180 gradi, e poi incollo, ottengo una striscia di Möbius, detta anche nastro o anello di Möbius, che non ha un fuori e un dentro.
Quelle che erano le due superfici del cilindro, separate dal bordo, ora sono in continuità, sono diventate una sola.
Questa volta la formica può raggiungere lo zucchero senza scavalcare il bordo, semplicemente andando avanti.
L’oggetto che abbiamo realizzato non ha un dentro e un fuori, ha una sola superficie.
Realizzare un nastro di Möbius è facilissimo: striscia di carta, ruotare un’estremità di 180 gradi, incollare.
Traccio un segno con la matita, partendo da un punto sulla superficie.
Scorro tenendo appoggiata la punta della matita sulla carta (come se fosse la formica): la matita traccia una linea.
Vado avanti senza staccare la punta dalla superficie della striscia. Dopo un lungo percorso mi ritrovo al punto di partenza: sulla striscia c’è un’unica linea che percorre l’intera superficie, da una parte e dall’altra; non ho scritto che la carta non ha più due parti, ho scritto che le due parti si trovano sulla stessa superficie (mi sembra di essere in classe).
Altre cose inaspettate, astonishing – direbbero gli inglesi – accadono tagliando il nastro lungo la linea che abbiamo tracciato.
Infilo le forbici in un punto e taglio seguendo la linea.
Accadono cose diverse se eseguo il taglio seguendo una linea mediana o seguendo una linea che si trova a un terzo della larghezza della striscia.
Provare per credere.
La striscia di Möbius si chiama così per ricordare il matematico tedesco August Ferdinand Möbius (1790 – 1868), che si occupò, tra i primi, di quella branca della matematica moderna che si chiama topologia e studiò le proprietà dell’anello appena descritto.
La topologia, in parole povere (e, conseguentemente, anche con un impoverimento concettuale), si occupa dello studio delle forme indipendente dalla misura (spero che l’associazione dei matematici non paghi un killer per punirmi di questa definizione semplificata).
Prima di Möbius un grande matematico svizzero, che noi italiani chiamiamo Eulero (Leonhard Euler, 1707 – 1783), si era occupato di topologia.
Eulero aveva trovato la soluzione di un problema utilizzando strumenti topologici: i grafi, costituiti da archi e nodi.
Il problema riguardava la città di Königsberg (oggi Kalinigrad, in Russia), attraversata dal fiume Pregel, che, con i suoi ponti e un’isola, la divide in quartieri.
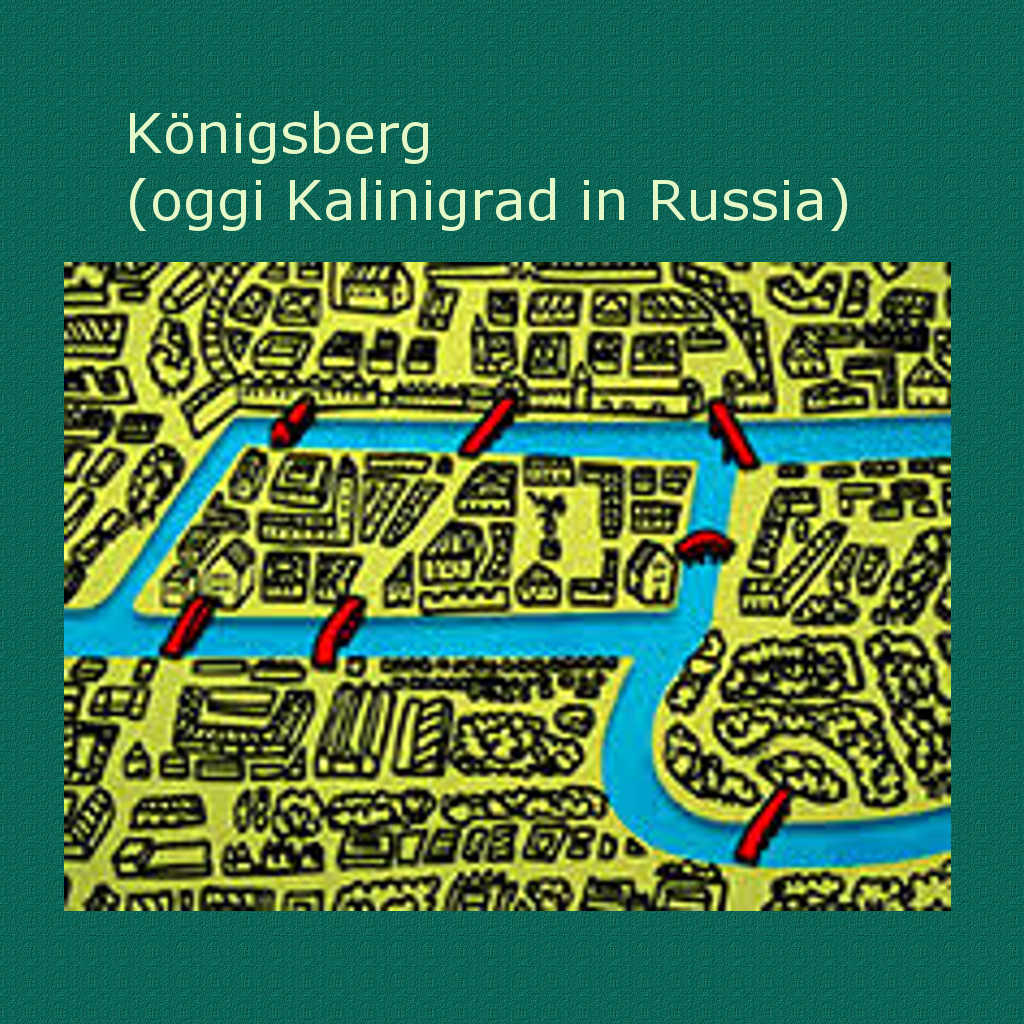
Problema: è possibile compiere un percorso che porti a visitare tutti i quartieri in cui è divisa la città, attraversando ciascun ponte, ma passando attraverso di esso una volta e una soltanto? (i matematici dicono: una e una sola volta)
Probabilmente agli abitanti di Königsberg – i cui posteri avrebbero patito vicissitudini tragiche dopo la fine della seconda guerra mondiale – non dava fastidio ripassare più volte sui ponti, anzi questa possibilità consentiva piacevoli incontri; forse anche fuori della città la cosa non destava grande interesse; forse il problema interessava solo al matematico che lo aveva posto.
L’obiettivo di Eulero non era di offrire uno strano giro turistico ai visitatori di Königsberg (slogan nell’agenzia: vedrai tutto una sola volta); voleva trovare un metodo che consentisse di risolvere tutta una serie di problemi dello stesso tipo senza usare la geometria classica (che riduce gli oggetti a forme astratte e ragiona sulle misure dei contorni, delle aree, dei volumi). Voleva usare la topologia, cioè la forma degli oggetti e le relazioni che collegano le loro parti. In sostanza voleva fare a meno delle misure.
Si tratta di un problema di flusso, cioè di oggetti che scorrono in una sola direzione (la persona che visita tutti i quartieri), lungo un percorso obbligato (i ponti da percorrere tutti una sola volta).
Ecco che un problema, apparentemente ozioso, diventa utile per risolverne altri, molto più importanti e concreti: per esempio lo snellimento del traffico in una grande città o lo scorrimento dell’acqua nei sistemi idraulici, o il controllo delle macchine, o il funzionamento di programmi informatici complessi (dovunque ci sia un flusso di oggetti reali o virtuali).
La topologia, come la matematica in generale, pone problemi astratti e cerca di risolverli, non solo per un gusto intellettuale, che pure basterebbe a giustificare l’impegno (sfidare la mente umana, spingerla sempre più in profondità), ma anche perché le sue scoperte portano benefici concreti alle scienze empiriche, all’ingegneria, alla tecnica.
Eulero elaborò un teorema: condizione necessaria e sufficiente affinché un grafo (rete di quartieri uniti da ponti) sia percorribile completamente partendo da un nodo (un quartiere), passando una e una sola volta per ciascun arco (ciascun ponte), è che esista un percorso fra ogni coppia di nodi (un ponte tra due quartieri) e che ogni nodo sia toccato da un numero pari di archi.
Semplice, no? Sarebbe potuto arrivarci chiunque. Quante volte abbiamo sentito al mercato le signore anziane con la borsa della spesa enunciare il teorema dei ponti per discutere tra loro la possibilità di fare un giro completo, passando una sola volta accanto a ogni bancarella, senza mancarne una! Quante volte! Quante? Mai.
Eulero non solo enunciò. Fece una cosa in più, fondamentale quando si parla di teoremi: la dimostrazione.
Un teorema non è un atto di fede o un dogma, non basta enunciarlo, bisogna dimostrarlo.
Diamo per buona la dimostrazione, che non si può rifare qui (potrebbe esserci un killer in agguato), ma sappiamo che regge.
Come lo sappiamo?
La dimostrazione del teorema dei ponti regge perché ha retto la prima volta in cui il professor Leonhard Euler l’ha illustrata ai suoi studenti, o a sé stesso, nella sua cameretta, sulla scrivania di legno o su quelle antiche, lunghe lavagne che si utilizzavano nelle aule di matematica. Le panche nell’edificio seicentesco erano disposte in semicerchio, in discesa; convergevano verso la cattedra, addossata a una parete coperta, in basso, dalle lavagne e da una porticina dalla quale appariva, all’improvviso, il professore. Mi sto confondendo, troppo tempo è passato; le panche in cerchio e la porticina erano nell’aula Minerva (aula di Fisica, edificio ottocentesco). Nell’Istituto di Matematica, austero, conventuale, seicentesco, le panche erano in discesa, ma non in semicerchio.
Scriviamo i simboli matematici con il gesso sulla lavagna, con la penna d’oca e l’inchiostro sulla carta o con la penna a sfera: la logica matematica è quella; se una dimostrazione ha retto la prima volta, reggerà sempre.
Se il professore ha commesso un errore (càpita), non solo lui, ma un suo collega, uno studente, un addetto alle pulizie avrebbe potuto accorgersi dell’errore, evidenziarlo con soddisfazione, apportare la correzione (mi viene in mente una bellissima scena di Will Hunting Genio ribelle (1997), regia di Gus Van Sant, con Robin Williams e Matt Damon). Non è come nelle scienze empiriche, i cui risultati dipendono dalla disponibilità e dall’evoluzione degli strumenti di misura.
Se non hai a disposizione otto radiotelescopi sparsi sulla terra, non puoi fotografare un buco nero. (Fotografare un buco nero? Ma che cazzo dici!? È un’espressione usata a scopo divulgativo? Soprattutto nella divulgazione si dovrebbe stare attenti al rigore delle espressioni utilizzate, perché chi le riceve non è in grado di decrittarle).
Anche gli strumenti del pensiero evolvono, però se sei Pitagora, e hai dimostrato che «la somma delle aree dei quadrati costruiti sui cateti … …», si potranno trovare altre dimostrazioni, ma la tua sarà sempre valida, se era valida quando l’hai enunciata (sbagliato spiegare il teorema di Pitagora facendo misurare i lati del triangolo: ci sono a disposizione dimostrazioni semplici ma efficaci).
Dal teorema dei ponti consegue che a Königsberg il problema era irrisolubile, perché non da tutti i nodi usciva un numero pari di archi. Naturalmente, anche qui si è semplificato, evitando di distinguere un cammino euleriano e un ciclo euleriano.
Si voleva solo sottolineare che gli strumenti della topologia utilizzati da Eulero per risolvere il problema dei ponti e i risultati di quei ragionamenti, sono stati, in seguito, impiegati in vari campi dell’ingegneria.
Il bello è che un problema astratto dev’essere risolto con mezzi astratti; ne consegue l’errore che, a volte, si compie nelle scuole, presentando la matematica ai bambini come se fosse una tecnica per aiutare a fare la spesa; presentata in questo modo, la matematica diventa odiosa.
Dopo tanti anni ho capito il motivo per il quale, alle scuole medie, odiavo la matematica.
In cuor mio me la prendevo con quel professore pelato e, nel ricordo, di colorito verdastro, che ce l’aveva con me (anch’io ce l’avevo con lui).
Poi sono passato dall’altra parte e ho capito come sia difficile cambiare le cose quando sei vincolato a programmi fatti non si sa da chi, basati sulla quantità, che prevedono controlli finali nei quali anche tu ti senti sotto controllo.
L’esame di terza media comprende una prova scritta che normalmente è unica per tutte le classi della scuola, a volte per tutte le classi del plesso. Devi, dunque, avere svolto un programma compatibile con il programma svolto da tutte le altre classi, altrimenti non potrai metterti d’accordo con gli altri insegnanti sui quesiti da proporre. Fra gli insegnanti c’è, naturalmente, quello, o, più spesso, quella (non è una precisazione maschilista ma solo statistica) che alza il ditino come faceva a scuola, quando era il primo o la prima della classe, e dice: «i miei alunni (enfasi su miei) hanno svolto questa applicazione fondamentale della matematica, prevista dalle indicazioni programmatiche; voglio che siano esaminati anche su di essa (l’italiano precario è testuale: ricavo il testo da vecchi diari)».
Fate esempi concreti, riferitevi all’esperienza degli alunni, motivateli mostrando le applicazioni, dicevano quelli che comandavano: gli esperti, i pedagoghi adorati dai ministri.
A fine anno arrivavano i rappresentanti delle case editrici («cambierete il libro di testo?»).
Poi ci si è messa l’informatica, perché qualcuno crede che il triangolo disegnato sullo schermo non sia una rappresentazione, come il triangolo disegnato con la matita o con il gesso, ma sia il concetto astratto di triangolo. Crede che il quadrato sullo schermo sia veramente quadrato.
Non sarebbe meglio puntare sulla qualità e non sulla quantità? Non sarebbe meglio inserire un insegnamento che si chiami Matematica (non Scienze matematiche … Educazione non so cosa o in altri modi fantasiosi), con l’obiettivo di far acquisire i concetti alla base della matematica, riservando ad altri insegnamenti la misura dei campi di grano (quelli della canzone di Lucio Battisti), il calcolo dell’interesse composto, la probabilità di vincere un terno al lotto giocando sulla ruota di Bari? L’esempio sul terno si riferisce sempre alla ruota di Bari. Ci dev’essere una ruota più grande delle altre a Bari.
Può darsi che qualcuno, riflettendo su quei concetti di base, lontani da ogni apparente utilità pratica immediata e dall’esperienza concreta e banale di tutti i giorni (se dovessimo studiare ciò che possiamo acquisire per esperienza, a che serve andare a scuola?), si appassioni a una scienza astratta che, senza darlo a vedere, ci ha portati sulla luna ed è entrata nelle nostre case con discrezione.
Torniamo al nastro di Möbius, alle sue proprietà inaspettate (astonishing); abbiamo capito che oggetti apparentemente fantastici sono sotto i nostri occhi: basta avere la capacità di scovarli e gli strumenti matematici per studiarli.
L’incisore olandese Maurits Cornelis Escher (1898 – 1972) aveva straordinarie capacità di osservazione e di rielaborazione delle forme attraverso le quali percepiamo la realtà; infatti rappresentò il nastro di Möbius in un disegno, con la famosa formica che si muove lungo l’intera unica superficie senza mai attraversare il bordo.
Il disegno di Escher è riprodotto sulla foto posta in testa a questo commento.
Partendo dai panorami, soprattutto italiani, che lo colpivano – la campagna toscana, le case di Ravello, le torri di San Gimignano, ecc. – Escher andò molto oltre con i suoi disegni (tecnicamente: xilografie), realizzati incidendo il legno e inchiostrando lo stampo.
Anche quando rappresentava elementi naturali e multiformi, come i pini o i tetti dei paesini italiani, gli interessava soprattutto, quasi esclusivamente, la struttura.
Dalle forme, che osservava con amore, risaliva alla struttura: la rappresentava, la modificava.In questo modo portò le sue xilografie a un livello sempre più alto di astrazione.

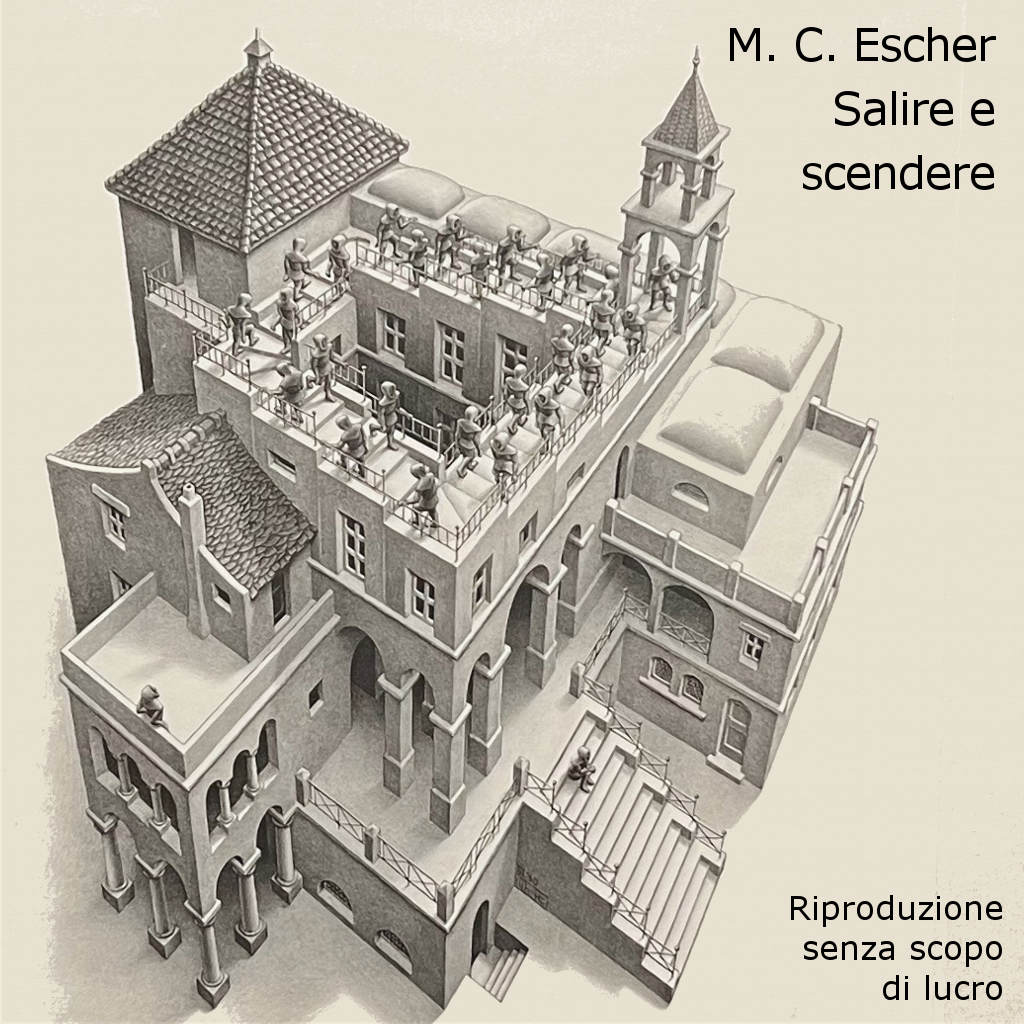
Realizzò disegni di architetture impossibili – oggetti che non hanno un sopra e un sotto, scale inserite in mondi diversi, percorse da due persone che vanno nella stessa direzione, ma una sale, l’altra scende; la sagoma di una persona è seduta comodamente su un parallelepipedo appoggiato su un piano verticale. Uno è giunto agli ultimi gradini di una scala che porta su una parete verticale, dove si trova un portone orizzontale rispetto a noi, ma anche rispetto al tizio che sta per raggiungerlo.
Come farà per entrare in casa? Una volta aperto il portone ci cade dentro.
Non solo non si trova nel nostro mondo, ma anche nel suo le cose non vanno tanto bene. Una scala in primo piano ha i gradini sui due lati, sopra e sotto. Questo sarebbe possibile, se fosse solo un fatto estetico; il problema è che viene percorsa su entrambi i lati.
L’albero nel giardino a destra è quasi orizzontale; si vede l’ombra. Una coppia è seduta a un tavolo poggiato sul piano obliquo (rispetto a noi, ma anche rispetto agli altri mondi che s’intersecano); la coppia sta pranzando; si vedono una bottiglia, un bicchiere, i piatti, il cestino con il pane. Evidentemente la gravità agisce in direzioni diverse.
Un altro giardino si trova in alto a sinistra, capovolto rispetto a quello in basso a destra; una coppia passeggia abbracciata, uno si affaccia su questa intersezione di piani, scale, persone. Un altro, in alto a destra, si affaccia sulla ringhiera, si sporge per guardare in basso, verso gli altri mondi.
Anche noi siamo capovolti rispetto agli abitanti dell’altro emisfero (e loro rispetto a noi), lo sappiamo, ma non li vediamo. Questi si guardano tra di loro e sembra che possano passare d’un balzo da un mondo all’altro. Una persona, inquadrata di spalle in primo piano, sale scale che si trovano nel nostro mondo, condivide con noi l’alto e il basso. Finalmente uno con il quale possiamo scambiare quattro chiacchiere, se si gira verso di noi quando ha raggiunto il pianerottolo, ma avremo molta paura a chiamarlo. Non sappiamo se questi alieni sono amichevoli.
Oggetti impossibili, come il belvedere a due piani, con la scala appoggiata all’interno del primo piano e all’esterno del piano superiore (le colonne, quindi le pareti esterne, sono allineate). In realtà tre colonne in primo piano sembrano verticali ma vanno verso l’interno. Però l’illusione ottica è perfetta, anche perché mascherata da altre colonne, alternate, realmente verticali e gli archi nascondono la mancanza di parallelismo.

Che dire dell’acqua di quella cascata che compie un percorso circolare, contraddicendo i principi della termodinamica e la conseguente impossibilità del moto perpetuo?

Il mondo di Escher è come il mondo del Mago di Oz, è come il mondo di Alice nel paese delle meraviglie, è come, trovandoci in periodo natalizio, il mondo del Grinch (commento al film 1/12/2018).
In questi disegni (incisioni) si parte dalla realtà per scoprire mondi fantastici o aspetti fantastici del mondo.
I disegni impossibili sono un aspetto del lavoro di Escher; un altro è la ripetizione di elementi che riempiono interamente lo spazio, dove non c’è più distinzione tra il primo piano e lo sfondo.

Lo sfondo può essere primo piano, il primo piano può essere sfondo.

Le metamorfosi – trasformazioni graduali e circolari che portano le forme viventi a diventare altre, a costruirsi dal nulla e ad evolversi, per poi tornare indietro e gradualmente perdersi nel nulla indistinto.


Il film documentario sulla vita di questo artista – che ho visto al cinema Spazio Uno in una bella serata prenatalizia, gelida come è naturale che sia una serata prenatalizia – si chiama, appunto: Viaggio nell’infinito (regia di Robin Lutz).
Quest’anno le illuminazioni sono state di mio gradimento; mi è piaciuto, in particolare, il cono metallico installato da Mimmo Paladino in piazza Santa Maria Novella; un po’ meno le installazioni dei suoi colleghi in altre due piazze.
Un giro per via Tornabuoni, piazza Strozzi, piazza della Repubblica, piazza Signoria, piazza Duomo, piazza Santa Maria Novella (giro limitato, per non allontanarmi troppo dal cinema) è stato una buona premessa alla visione di un film che racconta la vita di questo straordinario artista, attraverso le sue parole, i luoghi da lui abitati o visitati, l’intervista a due figli (uno di novantadue anni) e a persone che lo hanno conosciuto.
Molto interessanti anche alcune animazioni applicate ad opere di Escher, che si prestano bene a questo tipo di elaborazione.
I lavori di questo straordinario incisore interessarono molto la cultura pop degli anni ‘60 e ‘70; Escher morì nel 1972. Dopo un lungo periodo in cui era stato ignorato dalla critica d’arte e dal mercato, nell’ultimo decennio le sue opere avevano subito un balzo, nelle quotazioni di mercato e nella valutazione dei critici.
Mich Jagger gli aveva scritto una lettera piena di complimenti, che cominciava così:
«Caro Maurits, / Per un bel po’ di tempo ho avuto tra le mani il tuo libro, e non smetto mai di stupirmi ogni volta che lo sfoglio!».
Segue una lunga serie di apprezzamenti e la richiesta di poter utilizzare uno dei disegni, o uno nuovo, inedito, da mettere sulla copertina di un disco che i Rolling Stones stavano per pubblicare.
Mich Jagger chiarì anche i termini economici della richiesta, specificando che si sarebbe sicuramente trovato un accordo pienamente soddisfacente per l’autore.
Escher rispose come segue al responsabile dei Rolling Stones che faceva da tramite:
«Egregio Signore,
alcuni giorni fa ho ricevuto dal signor Jagger una lettera che mi chiede di disegnare un quadro o di mettere a disposizione un mio lavoro inedito da riprodurre sulla custodia per un LP. La mia risposta a entrambe le richieste deve essere no, in quanto voglio dedicare tutto il mio tempo e la mia attenzione ai tanti impegni che ho contratto. Non posso assolutamente accettare ulteriori incarichi o perdere tempo con la pubblicità. A proposito, la prego di dire al signor Jagger che non sono Maurits per lui, ma
Molto sinceramente,
M. C. Escher»
Qui il personaggio di Nino Manfredi, in una famosa Canzonissima, avrebbe aggiunto: piglia, pesa, incarta e porta a casa.
Escher diede una lezione di buona educazione, che è amore della forma, ma sotto alla forma si cela sempre una sostanza, al divo del rock forse abituato ad avere tutti ai suoi piedi e a trattare tutti come amici intimi, come compagnoni a cui appoggiare una mano sulla spalla, da chiamare col nome di battesimo come se ci fosse una confidenza di vecchia data.
La sua risposta è anche una lezione a tutti noi: bisogna credere nella propria arte e, se si ritiene di avere qualcosa da dire più importante del mercato sotto casa o del mercato dell’arte, non essere disposti a perdere tempo con la pubblicità.
È vero: è una battaglia contro i mulini a vento; è vero: morto l’autore, le opere di Escher sono state e sono le più sfruttate proprio dalla pubblicità che lui rifiutò, però un don Chisciotte serve ogni tanto per insegnarci che esistono confini che separano arte e mercato.
Non bisogna credere che Escher avesse un cattivo carattere o si rifiutasse di mettere la sua opera a disposizione degli altri.
Alla fine degli anni settanta Bruno Ernst pubblicò un libro sulle sue opere, (Lo specchio magico di M. C. Escher, Taschen editore), con molti riferimenti biografici, un libro al quale, negli ultimi anni di vita, nonostante le sofferenze dovute agli interventi chirurgici che dovette subire, accettò di dare la sua collaborazione.
Ho detto che negli anni sessanta e settanta Escher fu una vera icona (le sue opere furono un’icona) per la cultura pop.
Un altro cantante famoso volle conoscerlo e ci riuscì, forse perché trovò una modalità di approccio più educata, rispetto a Mich Jagger: Graham Nash (complesso folk rock Crosby, Stills, Nash & Young).
La prima volta che Nash riuscì a incontrarlo, iniziò la conversazione dicendo: la considero un grande artista.
Escher rispose: non sono un artista, sono un matematico.
Sicuramente non voleva essere incasellato in una delle correnti di arte cerebrale che hanno proseguito la loro involuzione fino a produrre come capolavoro una banana attaccata al muro con lo scotch.
Forse non voleva che le sue opere fossero fagocitate dai critici logorroici o dal mercato che pretende di decidere che cosa è arte in base alla disponibilità di qualche affarista a spendere un capitale per arredare la stanza da letto o la stanza da bagno.
Escher non era un matematico, ma aveva intuizioni matematiche ed era un artista.
I suoi disegni si vedono bene su carta, ma non perdono nulla se visti sullo schermo del computer o della televisione.
È uno dei pochi casi in cui la visione su uno schermo di dimensioni ridotte (senza esagerare) non causa danno alla percezione delle opere di un artista geniale e moderno, anticipatore di una forma d’arte che si trova particolarmente a proprio agio con i bit.

